Model 2:
Study the following bivariate and partial tables.
| Table 17a. | RACE AND VOTER TURNOUT | |||
| RACE | ||||
|---|---|---|---|---|
| Black | Black | |||
| Voted | 44% | 62% | ||
| Did not vote | 56% | 38% | ||
| (200) | (450) | |||
| Table 17b. | RACE AND VOTER TURNOUT BY EDUCATION | |||||
|---|---|---|---|---|---|---|
| EDUCATION LEVEL | ||||||
| College Graduates | Non-College Graduates | |||||
| Black | White | Black | White | |||
| Voted | 68% | 73% | 29% | 33% | ||
| Did not vote | 32% | 27% | 71% | 67% | ||
| (100) | (250) | (200) | (150) | |||
In the space below, interpret the effects of education on the original relationship between race and voter turnout.
Exercise 17-2Determine the partial correlation between X and Y with z held constant (controlled), then the partial correlation between Y and z with X held constant, using the following zero-order bivariate correlations: rxy = .40, rxz = .30, rzy = .10
1. rxy.z = _____________________________________________________________________________
2. ryz.x = _____________________________________________________________________________
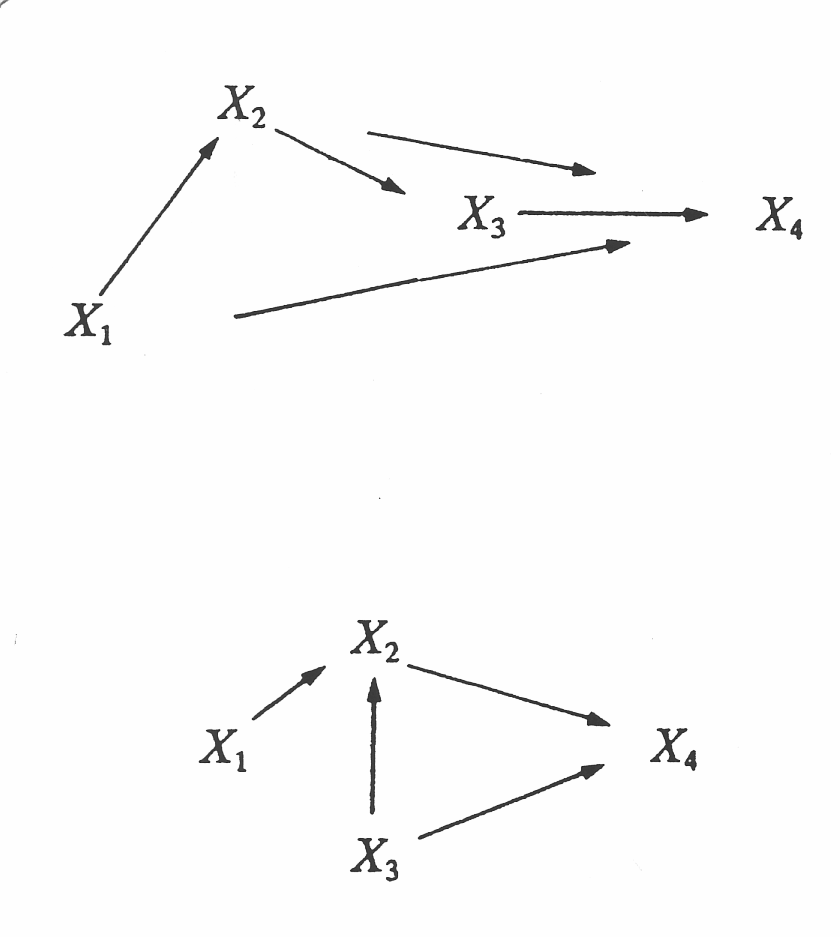
Write a set of equations in general form to describe the following causal systems, assuming that X1 is the independent variable, X2 and X3 are intervening variables, and X4 is the dependent variable.
Model 1:
Model 2: 
Use the following trivariate table to determine whether there is a relationship between religion and attitudes toward premarital sex. If there is a relationship, determine if and how the third variable, age, affects this relationship. Note that you will first have to collapse the table into a bivariate table to discover the relationship between religion and attitudes toward premarital sex. Then you can use the trivariate table to examine the effects of the third variable.
| AGE | |||||||
|---|---|---|---|---|---|---|---|
| Under-40 | 40 and over | ||||||
| Protestant | Catholic | rotestant | Catholic | ||||
| Attitude | |||||||
| Toward | Approve | 220 | 110 | 30 | 60 | ||
| Premarital | Disapprove | 180 | 90 | 270 | 540 | ||
| Sex | |||||||
| Total | 400 | 200 | 300 | 600 | |||