Page 34 - 2024-bfw-starnes-TPS7e-SE proofs.indd

SecTIoN 1c Displaying Quantitative Data with Graphs 21

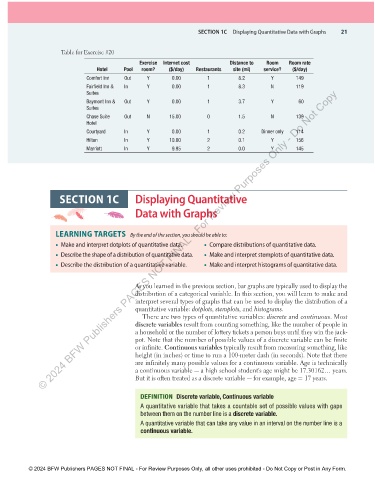
Table for Exercise #20
Exercise Internet cost Distance to Room Room rate
Hotel Pool room? ($/day) Restaurants site (mi) service? ($/day)
Comfort Inn Out Y 0.00 1 8.2 Y 149
Fairfield Inn & In Y 0.00 1 8.3 N 119
© 2024 BFW Publishers PAGES NOT FINAL - For Review Purposes Only - Do Not Copy
Suites
Baymont Inn & Out Y 0.00 1 3.7 Y 60
Suites
Chase Suite Out N 15.00 0 1.5 N 139
Hotel
Courtyard In Y 0.00 1 0.2 Dinner only 114
Hilton In Y 10.00 2 0.1 Y 156
Marriott In Y 9.95 2 0.0 Y 145

SECTION 1C Displaying Quantitative

Data with Graphs

LEARNING TARGETS By the end of the section, you should be able to:

• Make and interpret dotplots of quantitative data. • Compare distributions of quantitative data.

• Describe the shape of a distribution of quantitative data. • Make and interpret stemplots of quantitative data.

• Describe the distribution of a quantitative variable. • Make and interpret histograms of quantitative data.
As you learned in the previous section, bar graphs are typically used to display the
distribution of a categorical variable. In this section, you will learn to make and
interpret several types of graphs that can be used to display the distribution of a
quantitative variable: dotplots, stemplots, and histograms .
There are two types of quantitative variables: discrete and continuous . Most
discrete variables result from counting something, like the number of people in
a household or the number of lottery tickets a person buys until they win the jack-
pot. Note that the number of possible values of a discrete variable can be finite
or infinite. Continuous variables typically result from measuring something, like
height (in inches) or time to run a 100-meter dash (in seconds). Note that there
are infinitely many possible values for a continuous variable. Age is technically
a continuous variable — a high school student’s age might be 17.30162… years.

But it is often treated as a discrete variable — for example, age = 17 years.

DEFINITION Discrete variable, Continuous variable
A quantitative variable that takes a countable set of possible values with gaps
between them on the number line is a discrete variable.
A quantitative variable that can take any value in an interval on the number line is a
continuous variable.

© 2024 BFW Publishers PAGES NOT FINAL - For Review Purposes Only, all other uses prohibited - Do Not Copy or Post in Any Form.

02_StarnesTPS7e_40934_un01_p1_001_086_6pp.indd 21 13/09/23 5:37 PM