Page 34 - 2024-calc4e-SE proofs-4e.indd

Sullivan 04 apcalc4e 45342 ch02 166 233 5pp August 7, 2023 12:54

184 Chapter 2 • The Derivative and Its Properties

y 4/5 4/5
x 5 2 f (x) − f (2) (x − 2) − 0 (x − 2) 1
3 lim = lim = lim = lim 1/5 = −∞
x→2 − x − 2 x→2 − x − 2 x→2 − x − 2 x→2 (x − 2)
−
f (x) 5 (x 2 2) 4/5
2 f (x) − f (2) (x − 2) 4/5 − 0 (x − 2) 4/5 1
lim = lim = lim = lim = ∞
x→2 + x − 2 x→2 + x − 2 x→2 + x − 2 x→2 (x − 2) 1/5
+
1
f (x) − f (2) f (x) − f (2)
Since lim = −∞ and lim = ∞, we conclude that the
© 2024 BFW Publishers PAGES NOT FINAL - For Review Purposes Only - Do Not Copy.
1 3 4 x x→2 − x − 2 x→2 + x − 2
(2, 0) f has a cusp function f is not differentiable at 2. The graph of f has a vertical tangent line at the
21 at (2, 0)
point (2, 0), which is a cusp of the graph. See Figure 17.
Figure 17 f (2) does not exist; the
′
NOW WORK Problem 35.
point (2, 0) is a cusp of the graph of f .
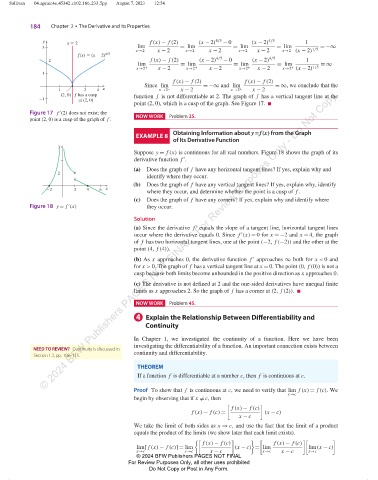
Obtaining Information about y = f(x) from the Graph
EXAMPLE 8
of Its Derivative Function
y
Suppose y = f (x) is continuous for all real numbers. Figure 18 shows the graph of its
derivative function f .
′
(a) Does the graph of f have any horizontal tangent lines? If yes, explain why and
2
identify where they occur.
(b) Does the graph of f have any vertical tangent lines? If yes, explain why, identify
22 2 4 6 x
where they occur, and determine whether the point is a cusp of f .
(c) Does the graph of f have any corners? If yes, explain why and identify where
′
Figure 18 y = f (x) they occur.
Solution
′
(a) Since the derivative f equals the slope of a tangent line, horizontal tangent lines
′
occur where the derivative equals 0. Since f (x) = 0 for x = −2 and x = 4, the graph
of f has two horizontal tangent lines, one at the point (−2, f (−2)) and the other at the
point (4, f (4)).
(b) As x approaches 0, the derivative function f approaches ∞ both for x < 0 and
′
for x > 0. The graph of f has a vertical tangent line at x = 0. The point (0, f (0)) is not a
cusp because both limits become unbounded in the positive direction as x approaches 0.
(c) The derivative is not defined at 2 and the one-sided derivatives have unequal finite
limits as x approaches 2. So the graph of f has a corner at (2, f (2)).

NOW WORK Problem 45.

4 Explain the Relationship Between Differentiability and
Continuity

In Chapter 1, we investigated the continuity of a function. Here we have been
investigating the differentiability of a function. An important connection exists between
NEED TO REVIEW? Continuity is discussed in
continuity and differentiability.
Section 1.3, pp. 108–115.
THEOREM
If a function f is differentiable at a number c, then f is continuous at c.

Proof To show that f is continuous at c, we need to verify that lim f (x) = f (c). We
x→c
begin by observing that if x 6= c, then
f (x) − f (c)

f (x) − f (c) = (x − c)
x − c
We take the limit of both sides as x → c, and use the fact that the limit of a product
equals the product of the limits (we show later that each limit exists).
f (x) − f (c) f (x) − f (c)

lim[ f (x) − f (c)] = lim (x − c) = lim lim(x − c)
x→c x→c x − c x→c x − c x→c
© 2024 BFW Publishers PAGES NOT FINAL
For Review Purposes Only, all other uses prohibited
Do Not Copy or Post in Any Form.